17. 连续概率分布
连续概率分布
在本课的下一部分中,Sebastian 将介绍如何以连续的概率分布进行可视化和计算。 在你继续学习之前,让我们再次回顾并比较一下离散和连续分布。
在本课一开始,我们向你展示了一个连续概率分布旁边的离散概率分布。 如下图所示:
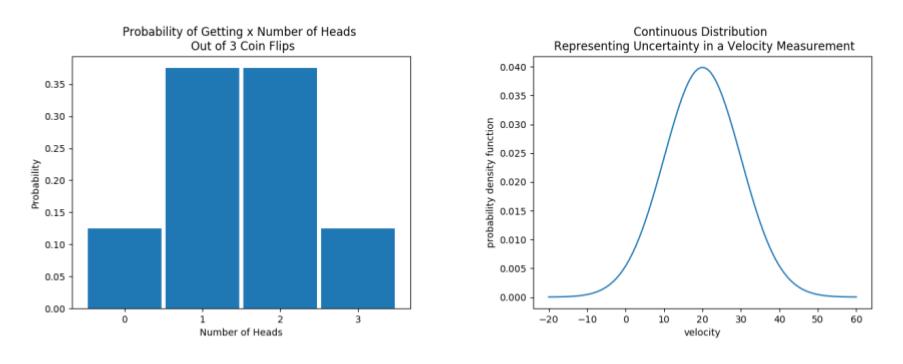
离散与连续概率分布
离散分布可以被分解成“片”。 每“片”代表一个结果,比如在硬币抛掷 3 次的例子中,有出现 0 次正面、 1 次正面、 2 次正面 和 3 次正面的不同情况 。
连续分布在整个 x 轴范围内都有一条连续不断的线。 比如,对于速度来说,你可以有 20 或 20.5 或 -10.451 的速度。
注意连续分布上的 y 轴标签:“概率密度函数”。 对于离散概率分布来说,y 轴表示事件发生的概率。 在连续情况下,概率密度函数并不直接表示概率; 相反,密度函数曲线下方的区域代表概率。
你将在本课的下一部分中了解更多信息。
不过,即使不知道“概率密度函数”意味着什么,你也可以从图表中了解到,速度大概在 20 左右,而速度大概在 0 或40 左右的可能性更小。
连续分布的特征
以下是连续分布和概率密度函数的一些特征。 在阅读本课的下一部分时,请牢记这些内容:
- y 值必须大于或等于 0。
- 发生于特定 x 值的概率可以等于 0。
- 两个 x 值之间发生事件的概率等于这两个 x 值之间的曲线下面积。
- 概率密度函数曲线下的总面积等于 1。
实际上,这些规则意味着速度等于 20 的概率为零。 对于连续分布,只能计算 19.99 和 20.01之间一系列值中的概率。
因为曲线下的总面积是 1,所以 “速度在负无穷和正无穷之间” 是有 100% 的可能性。
均匀连续分布
连续分布有许多不同类型: 连续概率分布列表的链接 。
但它们都具有上述相同的特征。 要计算连续分布的概率,必须计算曲线下的面积。 像上述可视化一样计算曲线下的面积需要微积分或软件程序。
所以 Sebastian 选择使用一种名为 均匀连续分布 的特定连续分布。 均匀连续分布形成一个矩形。 因此,你可以简单地通过基数乘以高度来计算曲线下面的面积。
下面是一个均匀连续概率分布的例子。 Sebastian 将解释更多关于这个分布的由来以及如何使用它的详情。
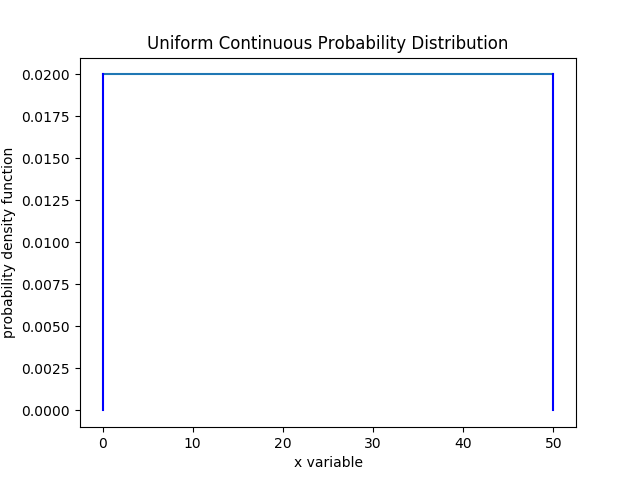
均匀连续分布
离散 vs 连续
SOLUTION:
- y 轴值必须大于或等于 0 。
- 总概率等于 1。